Más de una vez he tenido discusiones por mi opinión, claramente minoritaria, de que decir que Diplomacy es un juego sin azar es totalmente incorrecto. Pienso seguir insistiendo con eso.

Tipos de azar

Normalmente cuando hablamos de azar en juegos pensamos en dados o cartas. Hay otros elementos, pero al final son equivalentes a dados o cartas. Si en lugar de tirar un dado hacés girar una ruleta, es lo mismo. Y si tenés una bolsa llena de losetas y sacás una al azar, no hay diferencia con un mazo de cartas.

Por supuesto que a la hora de elegir elementos para un juego, no son exactamente lo mismo. Una ruleta puede tener ligeramente diferentes probabilidades dependiendo del área de cada posible resultado, mientras que un dado (no cargado) va a tener siempre las mismas probabilidades para cada cara (usando más de un dado podés tener otras distribuciones, también). Una bolsa con losetas tiene una sensación táctil que no tienen las cartas, mientras que un mazo de cartas permite acciones de manipular y previsualizar el orden futuro de las cartas.

Pero al final, resulta en que tradicionalmente tenemos dos formas de agregarle azar a un juego: un dado, que genera una secuencia de eventos independientes, o un mazo de cartas, que ordena un set de eventos.

Diplomacy, y las acciones simultáneas

Los jugadores dan instrucciones a cada una de sus unidades escribiendo un conjunto de «órdenes». El resultado de cada turno está determinado por las reglas del juego. No hay tiradas de dados ni otros elementos de azar.

Descripción de Diplomacy en BoardGameGeek (énfasis agregado)

Diplomacy es posiblemente la manera más divertida de perder amigos. Si tenés seis amigos y una tarde entera para dedicarle, es una experiencia interesante. Los elementos del juego son sencillos, y limitados en número. La clave del juego está en la negociación con los otros jugadores. No es posible que un jugador gane sin ayuda de otros, pero por otro lado sólo puede haber un ganador al final del juego.

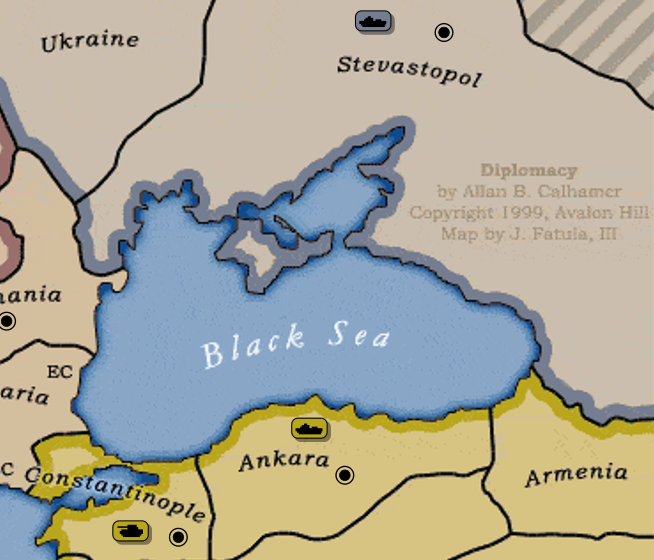
En cada turno, luego de una fase de negociaciones, cada jugador escribe en una hoja sus órdenes para sus unidades, y luego se revelan y resuelven simultáneamente. La resolución de combate no incluye dados ni cartas, cada ejército o flota tiene la misma fuerza, y gana el que consiga más apoyos de otros ejércitos o flotas, ya sea del mismo jugador u otro.

Desde el punto de vista tradicional, es cierto que no hay elementos de azar, como dados o cartas, ni tampoco ningún elemento equivalente. Pero eso no significa que no exista azar. El hecho de que las acciones sean simultáneas es en realidad un elemento de azar. Cuando vos decidís mover una flota de Ankara al Mar Negro, no sabés si tu oponente no está intentando mover de Sebastopol al Mar Negro también. El resultado de mi jugada es imposible de predecir, porque depende de qué haya jugado el otro jugador.

Go, piedra, papel, o tijera, y el asunto de los turnos simultáneos

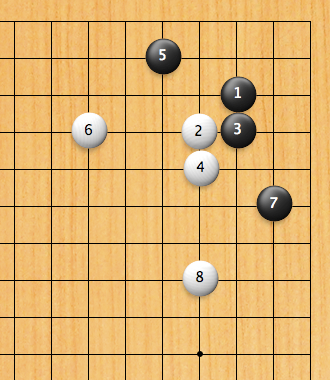
El argumento más común con el que me responden a esto es que vos podés, viendo la posición del tablero, saber qué va a jugar tu oponente. Asumiendo que el jugador es racional, y va a intentar maximizar sus chances de ganar, podés predecir qué va a jugar. Y si no juega lo mejor, bueno, de todas formas salís ganando, y sabés cómo responderle. Como un partido de go, o ajedrez, o algún otro juego abstracto del estilo.

En el go, tenés que tener en cuenta qué puede responder el oponente. Sabiendo qué puede llegar a jugar, podés pensar qué responderías vos, y así tener una secuencia en la cabeza que te diga si tu jugada es buena o es mala. Por supuesto que te podés equivocar, y puede resultar que al final la jugada no era buena. O que no tenés la experiencia o el entrenamiento para ver a dónde llega la secuencia. En cierta forma, se podría argumentar que hay también en el go un elemento de azar en ese sentido. Sé que ese grupo se puede matar, pero no estoy seguro cuál de las dos jugadas es la correcta. Pero ese azar no está introducido por las reglas del juego. Cuando hago una jugada, las consecuencias inmediatas de esa jugada son claras. Si juego una piedra en una intersección específica, el resultado inmediato es que hay una piedra en la intersección específica. Si doy la orden Ankara→Mar Negro, no puedo saber cuál es el resultado inmediato.

En cierta forma es similar al piedra, papel o tijera. Puedo elegir cualquiera de las tres jugadas, pero el resultado depende de qué elija mi oponente. Si supiera qué va a jugar mi oponente sería fácil. Es decir, de la misma manera que en el Diplomacy podría predecir qué va a jugar mi oponente basándome en cuál sería su mejor jugada, en el piedra papel o tijera podría predecir qué va a jugar mi oponente basándome en cuál sería su mejor jugada. El problema es que la mejor jugada de mi oponente depende de qué juegue yo. Y mi mejor jugada depende de qué juegue mi oponente.

Y ese es el tema con el Diplomacy. Es cierto que, como dicen quienes afirman que en el Diplomacy no hay elementos de azar, en la mayoría de las situaciones es posible predecir qué va a jugar el oponente. Pero no siempre.

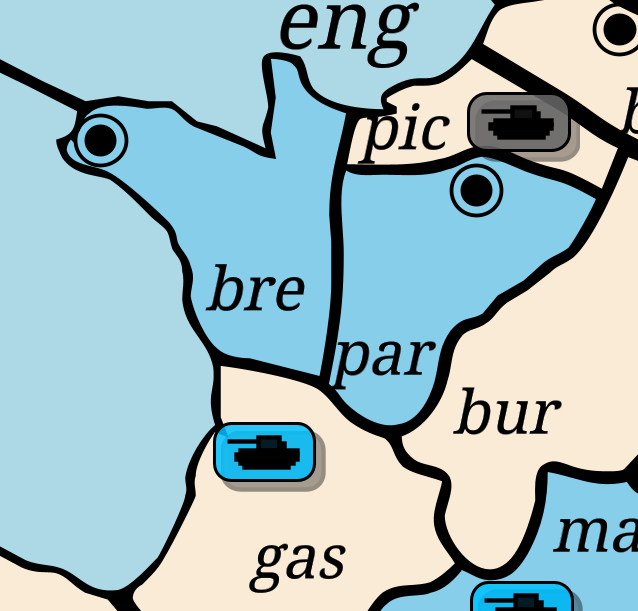
En el escenario de arriba, Francia puede defender Brest o Paris, pero no los dos. Alemania va a atacar a uno de los dos. ¿Cuál es la jugada correcta? Es imposible saberlo. Es, esencialmente, lo mismo que tirar una moneda.

Alguien muy terco podría decir que no son equivalentes. Que depende de la situación alrededor. Que capaz que Alemania prefiere Paris a Brest, por la razón que sea, y entonces la jugada correcta para Francia es defender Paris, sabiendo que es a donde va a intentar ir Alemania. Pero el problema con ese razonamiento es que si Alemania sabe que Francia sabe que Alemania prefiere Paris, entonces Alemania sabe que Francia va a defender Paris. Alemania prefiere Paris a Brest, sí. Pero prefiere Brest a ninguno de los dos, y si Alemania sabe que Francia va a defender Paris, entonces la jugada correcta es Brest. Entonces la jugada correcta de Francia es Brest, por lo que la jugada de Alemania es Paris, y entonces Francia va a Paris, entonces Alemania va a Brest, y estamos en el escenario de Vizzini de nuevo.

Por supuesto que no es lo mismo que en el piedra papel o tijera. Si, siguiendo en el ejemplo de arriba, Alemania prefiere Paris a Brest, si la preferencia es muy fuerte, capaz que Francia puede aceptar perder Brest para asegurarse de mantener Paris. La probabilidad de que Alemania vaya a Paris o Brest nunca va a ser 50% exacta. Pero no deja de ser al azar, de la misma manera que tirar dos dados y sumarlos no deja de ser al azar aunque la distribución ya no sea equiprobable.

Información oculta

El tema de las jugadas simultáneas es un caso específico de algo más grande. Si en lugar de ser simultáneo fuera secuencial, pero Alemania no sabe qué jugó Francia, el efecto sería el mismo. La cuestión no está tanto en lo simultáneo, sino en que el estado del juego no es completamente conocido para todos los jugadores. Otros juegos tienen un efecto similar sin la parte simultánea. Por ejemplo, en Starcraft los jugadores ponen órdenes boca abajo. Los oponentes saben que hay algo, pero no qué es. Pueden intentar deducir, pero nunca van a tener la certeza. Las decisiones que tomen en base a eso van a ser sobre un conocimiento inexacto del estado del juego.

Volviendo a ejemplos de dados y cartas, pensá en dos escenarios. En el primero, decidís la acción y luego tirás un dado y ves si el resultado te favorece. En el segundo, tirás el dado, y sin mirar qué salió, decidís la acción. Luego revelás el dado y ves si tu acción tuvo éxito o no. Obviamente son equivalentes. Pero por alguna razón siempre pensamos que la segunda opción tiene menos azar. Como el resultado del dado ya existe al momento de tomar la decisión, tendemos a creer que hay alguna forma de haberlo sabido, aunque no la hay. Y eso es esencialmente lo mismo que pasa con el Diplomacy, o el Starcraft, o muchos otros juegos.

Y a todo esto, ¿qué importa?

No, nada. La verdad es que es una discusión totalmente irrelevante. Pero es entretenida.